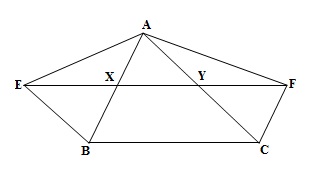
XY is a line parallel to side BC of a triangle ABC. If
![]()
and
![]()
meet XY at E and F respectively, show that ar(ABE)=ar(ACF).
Solution:
It is given that
![]()
![]()
(1)
Also, we have
![]()
(Given)
![]()
(2)
From (1) and (2), we can say that BEYC is a parallelogram.
(A quadrilateral is a parallelogram if both the pairs of opposite sides are parallel.)
Similarly, we can show that BXFC is a parallelogram.
Therefore, we have BEYC and BXFC as two parallelograms on the same base BC and between the same parallels EF and BC.
![]()
(3)
(Parallelograms on the same base and between the same parallels are equal in area.)
We can also see that
![]()
and parallelogram BEYC are on the same base BE and between the same parallels BE and AC.
![]()
(4)
Similarly, we have
![]()
and parallelogram BXFC on the same base CF and between the same parallels CF and AB.
![]()
(5)
From (3), (4) and (5), we can say that
![]()
Leave a Reply