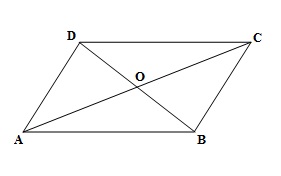
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Solution:
ABCD is a parallelogram having AC and BD as diagonals. AC and BD are meeting at O.
We know that diagonals of parallelogram bisect each other. It means that BO is the median of
![]()
.
![]()
(1)
(Median of a triangle divides it into two triangles of equal areas.)
Similarly, CO is the median of
![]()
.
![]()
(2)
Similarly, DO is the median of
![]()
.
![]()
(3)
From (1), (2) and (3), we can say that
![]()
Hence, we can say that diagonals of a parallelogram divide it into four triangles of equal area.
Leave a Reply