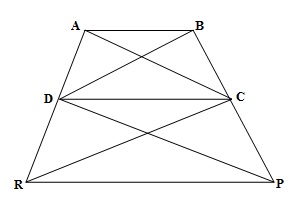
In Figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
Solution:
ABCD and DCPR are two quadrilaterals.
It is given that
![]()
(1)
We can also note that
![]()
and
![]()
are on the same base DC. (2)
From (1) and (2), we can say that
![]()
(3)
(Two triangles having the same base and equal areas lie between the same parallels.)
Similarly, it is given that
![]()
(4)
Subtracting (1) from (4), we get
![]()
![]()
(5)
We can also note that
![]()
and
![]()
are on the same base CD. (6)
From (5) and (6), we can say that
![]()
(7)
(Two triangles having the same base and equal areas lie between the same parallels.)
From (3) and (7), we can say that both the quadrilaterals ABCD and DCPR are trapeziums.
Leave a Reply