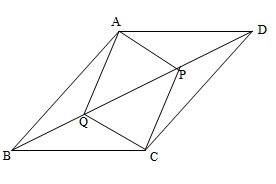
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Figure). Show that:
(i)
![]()
(ii) AP = CQ
(iii)
![]()
(iv) AQ = CP
(v) APCQ is a parallelogram
Solution (i)
In
![]()
and
![]()
, we have
DP=BQ (Given)
![]()
(Alternate Interior angles,
![]()
)
AD=BC (Opposite sides of parallelogram are equal)
Therefore, by SAS congruence rule,
![]()
Solution (ii)
We have already showed in solution (i) that
![]()
.
![]()
(Corresponding parts of congruent triangles are equal)
Solution (iii)
In
![]()
and
![]()
, we have
BQ=DP (Given)
![]()
(Alternate Interior angles,
![]()
)
AB=CD (Opposite sides of parallelogram are equal)
Therefore, by SAS congruence rule,
![]()
Solution (iv)
We have showed in solution (iii) that
![]()
![]()
(Corresponding parts of congruent triangles are equal)
Solution (v)
We have showed in solution (ii) and solution (iv) that AP=CQ and AQ=CP.
It means that APCQ is a paralleogram.
(If in a quadrilateral, each pair of opposite sides is equal, then it is a parallelogram.)
All the answers from this one is useful. I am always opened only this for maths solutions.
I do my all solutions of math with the help of my father, I know the solution but my solution is coming wrong. I agree with aditya that the answers are so useful.
this very use full in papers other vise …..