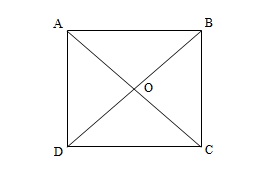
ABCD is a rectangle in which diagonal AC bisects
![]()
as well as
![]()
. Show that:
(i) ABCD is a square (ii) diagonal BD bisects
![]()
as well as
![]()
.
Solution (i)
Let’s suppose that we have rectangle ABCD in which diagonal AC bisects
![]()
as well as
![]()
.
We have AB=CD and BC=AD (Opposite sides of rectangle are equal) (1)
In
![]()
and
![]()
![]()
(Given)
AC=AC (Common)
![]()
(Given)
Therefore, by ASA congruence rule,
![]()
![]()
(Corresponding parts of congruent triangles are equal) (2)
From (1) and (2), we can say that ABCD is a rectangle having all the sides equal. It means that ABCD is a square.
Solution (ii)
In solution (i), we have showed that ABCD is a square.
Now in
![]()
and
![]()
BC=BA (Sides of square are equal)
BD=BD (Common)
CD=AD (Sides of square are equal)
Therefore, by SSS congruence rule,
![]()
![]()
(Corresponding parts of congruent triangles are equal) (3)
And,
![]()
(Corresponding parts of congruent triangles are equal) (4)
From (3) and (4), we can say that BD bisects
![]()
as well as
![]()
.
Leave a Reply