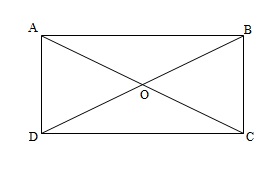
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
Let’s suppose that we have a parallelogram ABCD with AC=BC.
We need to prove that it is a rectangle.
In
![]()
and
![]()
![]()
(Given)
![]()
(Opposite sides of a parallelogram are equal)
![]()
(Common)
Therefore, by SSS congruence rule,
![]()
It means we have,
![]()
(Corresponding parts of congruent triangles are equal) (1)
But ,we also have
![]()
(Co-interior angles because
![]()
)
Putting (1) in the above equation, we get
![]()
![]()
![]()
Similarly, we can prove that all the angles of a given parallelogram ABCD are
![]()
but there is no need to do so because once we have proved that one angle is equal to
![]()
in a given parallelogram then it can be considered as rectangle.
Therefore, ABCD is a rectangle.
Leave a Reply