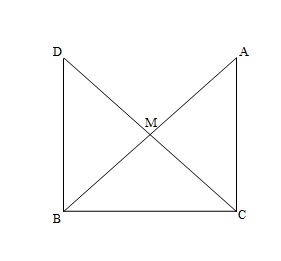
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Figure). Show that:
(i)
![]()
(ii)
![]()
is a right angle.
(iii)
![]()
(iv)
![]()
Solution (i)
In
![]()
and
![]()
![]()
(Given)
![]()
(Vertically Opposite Angles)
MC=MD (Given)
Therefore, by SAS rule,
![]()
Solution (ii)
From solution (i), we know that
![]()
Therefore,
![]()
(Corresponding parts of congruent triangles are equal)
But, these are alternate interior angles which means that
![]()
![]()
means that
![]()
(Co-Interior Angles)
![]()
![]()
Solution (iii)
In
![]()
and
![]()
, we have
BD=CA (Corresponding parts of congruent triangles,
![]()
and
![]()
)
![]()
(Proved in solution (ii))
BC=CB (Common)
Therefore, by SAS rule,
![]()
Solution (iv)
From solution (iii), we know that
![]()
Therefore, AB=DC (Corresponding parts of congruent triangles are equal)
![]()
![]()
(It is given that MD=CM)
![]()
![]()
Leave a Reply