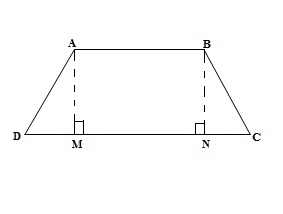
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Solution:
It is given that ABCD is a trapezium with
![]()
and
![]()
We need to prove that ABCD is a cyclic quadrilateral.
Construction: Draw
![]()
and
![]()
.
In
![]()
and
![]()
, we have
![]()
(Given)
![]()
(Each equal to
![]()
)
![]()
(Distance between two parallel lines is constant.)
Therefore, by RHS congruence rule, we have
![]()
![]()
(Corresponding parts of congruent triangles are equal) (1)
We also have
![]()
(Co-interior angles,
![]()
) (2)
From (1) and (2), we can say that
![]()
![]()
ABCD is a cyclic quadrilateral.
(If the sum of a pair of opposite angles of a quadrilateral is
![]()
, the quadrilateral is cyclic.)
Leave a Reply