Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i)
![]()
Comparing equation
![]()
with
![]()
and
![]()
with
![]()
, we get
![]()
and
![]()
![]()
and
![]()
We have
![]()
which means that equations have infinite many solutions because they are coincident.
Hence they are consistent.
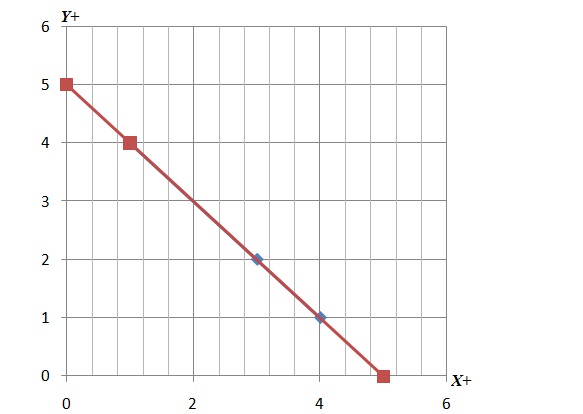
To represent equations graphically, we will plot both of the lines.
We plot the points for both of the equations to find the solution.
![]()
(Blue) and
![]()
(Red)
We can see that both of the lines coincide. Hence, there are infinite many solutions. Any point which lies on one line also lies on the other. Hence, by using equation
![]()
, we can say that
![]()
We can assume any random values for y and can find the corresponding value of x using the above equation. All such points will lie on both lines and there will be infinite number of such points.
(ii)
![]()
Comparing equation
![]()
with
![]()
and
![]()
with
![]()
, we get
![]()
and
![]()
![]()
and
![]()
We have
![]()
Lines are parallel to each other which means they have no solution.
Therefore, equations are inconsistent.
(iii)
![]()
Comparing equation
![]()
with
![]()
and
![]()
with
![]()
, we get
![]()
and
![]()
![]()
and
![]()
We have
![]()
![]()
, which means that they have unique solution.
Hence, they are consistent.
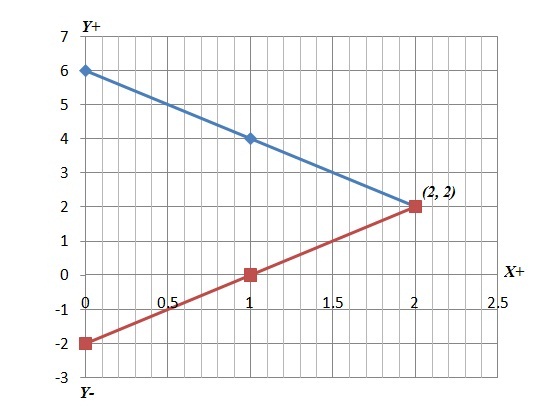
To obtain solution graphically, we will plot both of the lines.
We plot the points for both of the equations to find the solution.
![]()
(Blue) and
![]()
(Red)
We can clearly see that lines are intersecting at (2, 2) which is the solution.
(iv)
![]()
Comparing equation
![]()
with
![]()
and
![]()
with
![]()
, we get
![]()
and
![]()
![]()
and
![]()
![]()
Therefore, we have
![]()
The lines are parallel which means that they have no solution.
Hence, the equations are inconsistent.


Leave a Reply