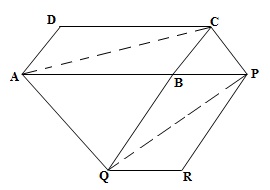
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see figure). Show that ar(ABCD)=ar(PBQR).
[Hint: Join AC and PQ. Now compare ar(ACQ) and ar(APQ)]
Solution:
It is given that ABCD and PBQR are two parallelograms.
We need to show that ar(ABCD)=ar(PBQR)
Construction: Join AC and PQ.
We have
![]()
(Triangles on the same base and between the same parallels are equal in area.)
![]()
![]()
![]()
![]()
(Diagonal of parallelogram divides it into two triangles of equal areas.)
Leave a Reply