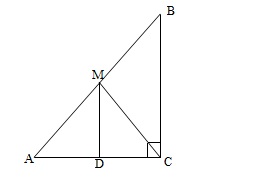
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC (ii)
![]()
(iii)
![]()
Solution (i)
It is given that M is the mid-point of side AB and
![]()
.
Therefore, by converse of mid-point theorem, D is the mid-point of side AC.
(The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.)
Solution (ii)
It is given that
![]()
and
![]()
(1)
We have
![]()
(2) (Corresponding angles)
From (1) and (2), we get
![]()
![]()
.
Solution (iii)
In
![]()
and
![]()
, we have
![]()
(Common)
![]()
(Each equal to
![]()
)
![]()
(D is the mid-point of AC as proved above in solution (i))
Therefore, by SAS congruence rule, we have
![]()
![]()
(Corresponding parts of congruent triangles are equal) (3)
It is given that M is the mid-point of side AB which means that
![]()
(4)
From (3) and (4), we can say that
![]()
Leave a Reply