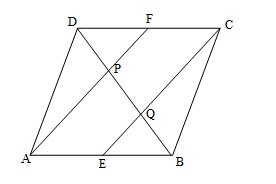
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see figure). Show that the line segments AF and EC trisect the diagonal BD.
Solution:
It is given that ABCD is a parallelogram.
![]()
and
![]()
(1)
(Opposite sides of parallelogram are parallel and equal)
From (1), we can say that
![]()
(2)
And,
![]()
![]()
(F and E are mid-points of CD and AB respectively) (3)
From (2) and (3), we can say that
AECF is a parallelogram. (A quadrilateral is a parallelogram if one pair of opposite sides is equal and parallel)
In
![]()
, we have
![]()
(AECF is a parallelogram) (4)
And, F is the mid-point of DC (Given) (5)
From (4) and (5), we can say that by converse of mid-point theorem, P is the mid-point of DQ.
(The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.)
Hence, DP=PQ. (6)
In
![]()
, we have
![]()
(AECF is a parallelogram) (7)
And, E is the mid-point of AB (Given) (8)
From (7) and (8), we can say that by converse of mid-point theorem, Q is the mid-point of BP.
(The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.)
Hence, BQ=PQ (9)
From (6) and (9), we get
![]()
which means that AF and EC trisect the diagonal BD.
Leave a Reply