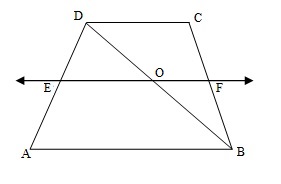
ABCD is a trapezium in which
![]()
, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the mid-point of BC.
Solution:
![]()
(Given) (1)
![]()
(Given) (2)
From (1) and (2), we have
![]()
![]()
In
![]()
, E is the mid-point of AD and
![]()
(Given)
Therefore, by converse of mid-point theorem, O is the mid-point of BD.
(The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.)
In
![]()
, O is the mid-point of BD and
![]()
. (Proved above)
Therefore, by converse of mid-point theorem, F is the mid-point of BC.
(The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.)
Leave a Reply