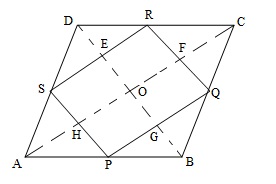
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
It is given that ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively.
We need to show that PQRS is a rectangle.
Let’s join AC and BD. AC meets SP at H and RQ at F. BD meets PQ at G and SR at E
In
![]()
, S is the mid-point of DA and R is the mid-point of DC.
Therefore, by midpoint theorem, we have
![]()
and
![]()
. (1)
Similarly, we have
![]()
and
![]()
by mid-point theorem. (2)
From (1) and (2), we can say that
![]()
and
![]()
![]()
is a parallelogram.
(A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.)
We have
![]()
which means that
![]()
. (3)
Also, we have
![]()
by mid-point theorem which means that
![]()
. (4)
From (3) and (4), we can say that ERFO is a parallelogram.
(A quadrilateral is a parallelogram if both pairs of opposite sides are parallel.)
But, we have
![]()
because diagonals of rhombus bisect each other at
![]()
. (5)
And, we have
![]()
(Opposite angles of parallelogram are equal) (6)
From (5) and (6), we can say that
![]()
It means that PQRS is a parallelogram (as proved above) having
![]()
. It is enough to consider PQRS as rectangle. Therefore, PQRS is a rectangle.
Leave a Reply