Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
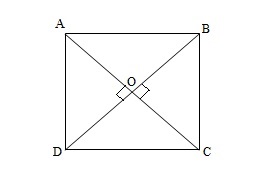
Let’s suppose that we have a quadrilateral ABCD with AO=OC, BO=OD, AC=BD and its diagonals AC and BD meet each other at
![]()
.
We need to show that it is a square.
In
![]()
and
![]()
AO=CO (Given)
![]()
(Each given equal to
![]()
)
BO=DO (Given)
Therefore, by SAS congruence rule,
![]()
.
![]()
(Corresponding parts of congruent triangles are equal)
But, these are alternate interior angles which means that
![]()
. (1)
Similarly, we can prove that
![]()
(2)
From (1) and (2), we can say that quadrilateral ABCD is a parallelogram. Hence, we have AB=CD and BC=AD because opposite sides of a parallelogram are equal. (3)
Now, in
![]()
and
![]()
AO=AO (Common)
![]()
(Each given equal to
![]()
)
OB=OD (Given)
Therefore, by SAS congruence rule, we have
![]()
![]()
(Corresponding parts of congruent triangles are equal) (4)
In
![]()
and
![]()
AC=BD (Given)
AD=BC (Proved above in (1) )
CD=DC (Common)
Therefore, by SSS congruence rule,
![]()
![]()
(Corresponding parts of congruent triangles are equal) (5)
But, we also have
![]()
(Co-Interior angles) (6)
From (5) and (6), we can say that
![]()
![]()
![]()
(7)
From (3), (4) and (7), we can say that ABCD is a parallelogram having all the sides equal and we have showed that it’s one angle is equal to
![]()
which is enough to consider it a square. Therefore, ABCD is a square.
Leave a Reply