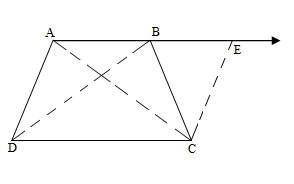
ABCD is a trapezium in which
![]()
and AD=BC (see figure). Show that
(i)
![]()
(ii)
![]()
(iii)
![]()
(iv) diagonal AC=diagonal BD
Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.
Solution (i)
ABCD is a trapezium in which we have AD=BC.
By construction, we extend AB and draw a line CE parallel to AD. (1)
We already have
![]()
because ABCD is a trapezium.
![]()
(2)
From (1) and (2), we can say that AECD is a parallelogram.
(A quadrilateral is a parallelogram if both the pairs of opposite sides are parallel.)
We have AD=BC (Given) (3)
Also, we have AD=CE (Opposite sides of parallelogram are equal) (4)
From (3) and (4), we can say that BC=CE
![]()
(In triangle, angles opposite to equal sides are equal) (5)
We have
![]()
(Co-Interior angles,
![]()
) (6)
And,
![]()
(Linear pair) (7)
From (6) and (7), we can say that
![]()
Using (5) in the above equation, we get
![]()
![]()
Solution (ii)
We have showed in solution (i) that
![]()
(8)
But, we have
![]()
(Opposite angles in parallelogram are equal) (9)
And,
![]()
(Alternate Interior angles,
![]()
) (10)
Using (9) and (10) in equation (8), we get
![]()
![]()
Solution (iii)
Join AC and BD.
In
![]()
and
![]()
BC=AD (Given)
![]()
(Proved above)
AB=BA (Common)
Therefore, by SAS congruence rule, we have
![]()
.
Solution (iv)
We showed in solution (iii) that
![]()
![]()
(Corresponding parts of congruent triangles are equal)
Best site for maths problems