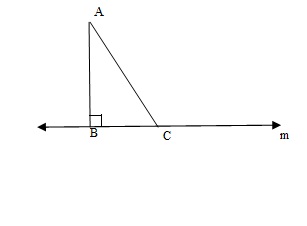
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Solution:
Let’s suppose that we have line
![]()
. A is any point from where we draw perpendicular AB to line
![]()
. Suppose there is any other random point C present on the line
![]()
. Join A and C.
So, we have
![]()
right angled at B.
We need to prove that AB is shorter than AC.
![]()
(AB is perpendicular to line
![]()
) (1)
![]()
(Angle sum property of triangle)
Putting (1) in the above equation, we get
![]()
![]()
![]()
and
![]()
It means that
![]()
is the largest angle in
![]()
.
Therefore,
![]()
(In any triangle, the side opposite to the larger angle is longer.)
Similarly, we can choose any random point present on line
![]()
and can complete a triangle in the same way. AB would be shortest of all the line segments. We can prove this using the same method.
Leave a Reply