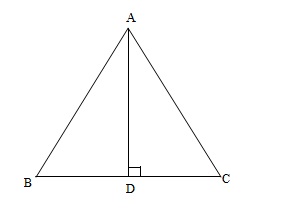
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects ∠ A.
Solution (i)
It is given that
![]()
is isosceles with AB=AC and AD is perpendicular to BC.
We need to prove that BD=CD.
In
![]()
and
![]()
, we have
![]()
(Given)
![]()
(Each given equal to
![]()
)
![]()
(Common)
Therefore, by RHS congruence rule,
![]()
Hence, we have BD=CD (Corresponding parts of congruent triangles are equal).
Solution (ii)
We have proved above that
![]()
.
It means that
![]()
(Corresponding parts of congruent triangles are equal).
![]()
means that AD bisects
![]()
.
Leave a Reply