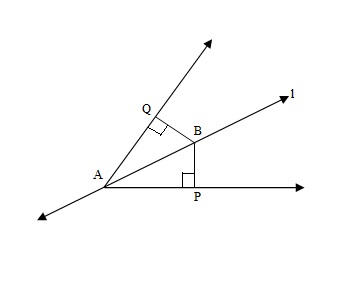
Line
![]()
is the bisector of an
![]()
and B is any point on
![]()
. BP and BQ are perpendiculars from B to the arms of
![]()
(See figure). Show that:
(i)
![]()
(ii) BP=BQ or B is equidistant from the arms of
![]()
.
Solution (i)
In
![]()
and
![]()
, we have
![]()
(It is given that AB is the bisector) (1)
![]()
(Common) (2)
![]()
(Each equal to
![]()
) (3)
Therefore, by AAS congruence rule, we have
![]()
.
Solution (ii)
From solution (i), we know that
![]()
.
Therefore, BP=BQ (Corresponding parts of congruent triangles are equal)
a very good site thank you