If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Solution:
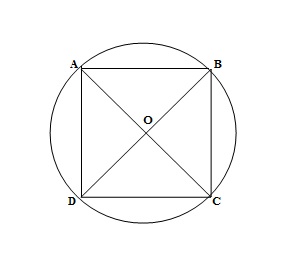
It is given that ABCD is a cyclic quadrilateral. Also, AC and BD are two diameters of circle having centre O.
We need to prove that ABCD is a rectangle.
BD is a diameter which means that
![]()
(1)
(Angle in a semi-circle is equal to
![]()
)
Similarly, AC is a diagonals which means that
![]()
(2)
(Angle in a semi-circle is equal to
![]()
)
From (1) and (2), we can notice that opposite angles of quadrilateral ABCD are equal which makes it a parallelogram.
Also, all the corner angles are equal to
![]()
which makes it a rectangle.
Leave a Reply