Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:
Let’s suppose that these two circles have centres O and O’ respectively.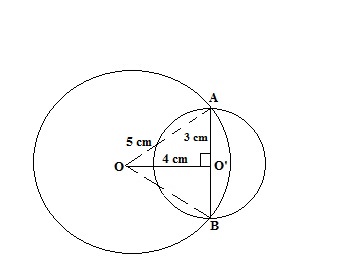
Join O and O’ to get a straight line segment OO’ which is given equal to 4 cm.
Draw
![]()
where A is any point present on the circumference of the smaller circle. AO’ is extended to intersect the smaller circle at point B. So, we have AB as diameter of the smaller circle. We are also given that O’A = 3 cm which is the radius of the smaller circle. At this point, we do not know that points A and B also lie on the circumference of the bigger circle.
We can find the length of OA using Pythagoras theorem.
Using Pythagoras theorem, we can say that
![]()
![]()
![]()
![]()
cm
At this point, we can note that OA is coming equal to the radius of the bigger circle. Therefore, A is the common point of contact of two circles.
Similarly, B is the common point of contact of two circles. It means that AB which is the diameter of the smaller circle, is also the common chord of two circles.
Hence, length of AB
![]()
cm
Leave a Reply