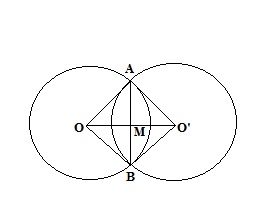
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
Draw two circles with centres O and O’. Join A and B to get a common chord AB. Join O and O’ with the mid-point M of AB.
We need to prove that centres lie on the perpendicular bisector of the common chord. In other words, we need to prove that OO’ is a straight line and
![]()
.
In
![]()
, M is the mid-point of chord AB.
![]()
. (1)
(The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.)
Similarly, in
![]()
, M is the mid-point of chord AB.
![]()
(2)
(The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.)
From (1) and (2), we can say that
![]()
which means that OO’ is a straight line and we can say that centres lie on the perpendicular bisector of the common chord.
Leave a Reply