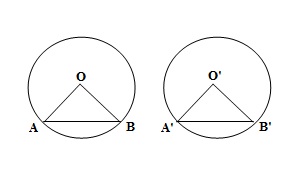
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Solution:
We have two congruent circles with centres O and O’ respectively. They are congruent which means that they have same radii.
It is also given that
![]()
We need to prove that they subtend equal angles at their centres. In other words, we need to prove that
![]()
In
![]()
and
![]()
, we have
![]()
(Congruent circles have same radii)
![]()
(Given)
![]()
(Congruent circles have same radii)
Therefore, by SSS congruence rule, we have
![]()
.
![]()
(Corresponding parts of congruent triangles are equal.)
It means that equal chords of congruent circles subtend equal angles at their centres.
Leave a Reply