Polynomials are the algebraic expressions in which all the variables have exponents as whole numbers.
Let’s take an example, we have algebraic expression:
![]()
Above algebraic expression is polynomial because each variable (
![]()
and
![]()
) has exponent which is a whole number.
So, polynomials are made up of individual terms. In the example written above, we have polynomial
(
![]()
) consisting of 4 terms.
1st term
![]()
2nd term
![]()
3rd term
![]()
4th term
![]()
Each term has variable, coefficient and exponent associated with it.
For term
![]()
, the variable is
![]()
, coefficient is 1 and exponent is 2.
For term
![]()
, the variable is
![]()
, coefficient is 1 and exponent is 2
For term
![]()
, the variable is
![]()
, coefficient is 1 and exponent is 1.
For term
![]()
, the variable is
![]()
, coefficient is -4 and exponent is 3.
Can you write few examples of polynomials?
(i)
![]()
(ii)
![]()
(iii) 3 (It is polynomial because it can be written as
![]()
, it is also called constant polynomial.)
(iv)
![]()
(v)
![]()
(vi)
![]()
(vii)
![]()
(viii)
![]()
Can you write few algebraic expressions which are not polynomials?
(i)
![]()
(Exponent of variable
![]()
is not a whole number)
(ii)
![]()
(Exponent of variable
![]()
is not a whole number)
(iii)
![]()
(Exponent of variable
![]()
is not a whole number)
(iv)
![]()
(Exponent of variable
![]()
is not a whole number)
(v)
![]()
(Exponent of variable
![]()
is
![]()
which is not a whole number)
At this point, you should be able to answer correctly if the given algebraic expression is polynomial or not.
It is good to know that polynomials consisting of just a single term are called monomials. For example :
![]()
and
![]()
are all monomials.
Polynomial consisting of two terms is called binomial. For example:
![]()
and
![]()
are examples of binomials.
Polynomials consisting of three terms are called trinomials. For example:
![]()
and
![]()
are examples of trinomials.
0 is also a polynomial called zero polynomial. We get zero polynomial if all the coefficients are equal to zero.
In the next article, we will be discussing about the degree of polynomials.
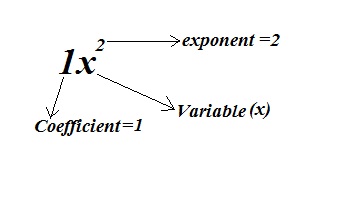
Leave a Reply