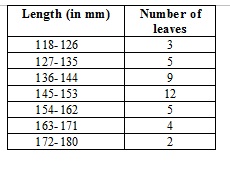
The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and the data obtained is represented in the following table:
Find the median length of the leaves.
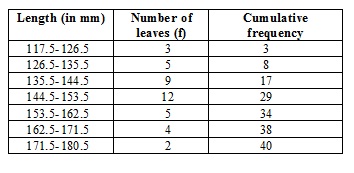
(Hint: The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5-126.5, 126.5-135.5, …, 171.5-180.5.)
Solution:
Intervals are not continuous. So, we will have to make them continuous.
The difference between two consecutive class intervals is 1.
So, we will subtract 0.5 from the lower limits and add 0.5 to the upper limits of classes.
Cumulative frequency greater than
![]()
is 29.
So, median class = 144.5-153.5
Median
![]()
where, l = lower limit of median class = 144.5
n = number of observations = 40
cf = cumulative frequency of class preceding the median class = 17
f = frequency of median class = 12
h = class size (assuming class size to be equal) = 9
![]()
Median
![]()
![]()
mm
Leave a Reply